Reference > Functions > SUM function

Adds the result of the argument to the previous result. This function is useful for evaluating Taylor series.

The SUM function differs from all other functions in 2 respects:

You are limited to 10 SUM functions in any equation (or pair of equations in the case of X=f(T),Y=g(T)).

The Prevent divide by zero errors feature of the Y=f(X) command and similar commands must be ignored when SUM is used in an equation. Division by 0 or other math error will result in an error message rather than incrementing X by a small value and re-evaluating.

Example

A well-known (though very slow to converge) method for calculating π is:

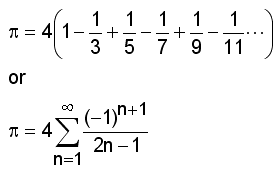
which can be expressed in DPlot as:

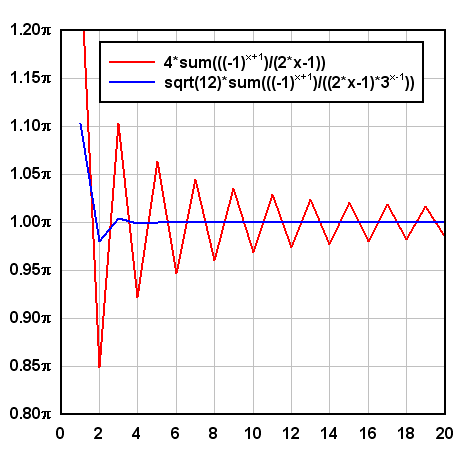
4*sum(((-1)^(x+1))/(2*x-1))

The mathematician and astronomer Madhava of Sangamagrama found a series that converges much faster than the above:

which may be expressed in DPlot as

sqrt(12)*sum(((-1)^(x+1))/((2*x-1)*3^(x-1)))

The first 20 terms of both series result in:

PI approximations, Taylor series

____________________________