Reference > Functions > BESSELJ function

BESSELJ(x,order) returns the Bessel function of the first kind at x for the specified order. The Bessel functions of the first kind are defined as the solutions to the Bessel differential equation

which are nonsingular at the origin. They are sometimes also called cylinder functions or cylindrical harmonics.

The n-th order Bessel function of x is:

where:

is the Gamma function.

The plot below shows the Bessel function for n=0,1,2,3,4,5.

BESSELJ function

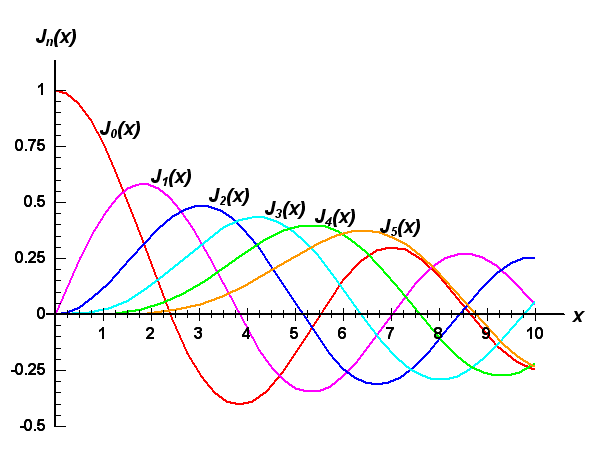
Order must be greater than or equal to 0. If order is not an integer, it is truncated. x must be greater than or equal to 0.

For more information on the Bessel function see the reference at MathWorld

____________________________